1 气体涡轮流量计的组成

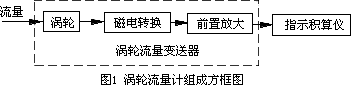
    如图1所示，气体涡轮流量计主要由涡轮流量变送器和指示积算仪组成[1]。涡轮流量变送器把流量信号转换成电信号，由指示积算仪显示被测介质的体积流量和流体总量。

    2 气体涡轮流量计的工作原理

    流体流经传感器壳体，由于叶轮的叶片与流向有一定的角度，流体的冲力使叶片具有转动力矩，克服摩擦力矩和流体阻力矩之后叶片旋转，在力矩平衡后转速稳定，在一定条件下，转速与流速成正比，由于叶片具有导磁性，它处于信号检测器（由永久磁钢和线圈组成）的磁场中，旋转的叶片切割磁力线，周期性地改变线圈地磁通量，从而使线圈两端感应出电脉冲信号，此信号经过放大器的放大整形，形成有一定幅度的连续的矩形波，可远传至显示仪表，显示出流体的体积流量或总量。

    3 气体涡轮流量计仪表系数的理论表达式

    作用在涡轮上的力矩可分为以下几个：流体通过涡轮时对叶片产生的切向推动力矩M1；流体沿涡轮表面流动时产生的粘滞摩擦力矩M2；轴承的摩擦力矩M3；磁电转换器对涡轮产生的电磁反作用阻力矩M4。

    由此可建立涡轮的运动微分方程：

           （1）

    式中：J为涡轮的转动惯量；ω为涡轮的旋转角速度；τ为时间。

    当流量恒定时，涡轮达到匀速转动，，所以M1= M2 + M3 + M4。根据文献[2]，推动力矩可表示为：

    M1 = a1qv2 - a2ωqv                （2）

    式中：a1、a2为与涡轮传感器结构和流体密度有关的系数；qv为流量，L/s。

    由于涡轮流量计在量程范围内属于紊流工作区，固以下计算只考虑紊流时的情况。反作用力矩中的M2，在紊流时可近似表示为：

    M2 = a3qv2                            （3）

    通常M3和M4相对于M2比较小，但为了提高计算精度，这里根据文献[3]推导出了它们的表达式：

    M 3 = a4ω2/3                    （4）

    M4 = a5ω3                           （5）

    分别将式（2）、（3）、（4）、（5）带入式（1）并经整理可得：

    qv2 - a6ωqv = a7ω2/3 + a8ω3    （6）

    式中：a6、a7、a8为经整理后的综合系数。

    通过以上的推导过程可以看出，涡轮的流量与转速并不是简单的线性关系。相互之间是一个比较复杂的高次表达式关系。

    4 气体涡轮流量计仪表系数的计算方法

    表1 某一涡轮流量计出厂校验数据

    由式（6）可以看出，涡轮的流量与转速的关系比较复杂。为了简化应用，通常省略影响比较小的等式右边部分，这样即可得出一个线性表达式，将角速度转换为频率后即为qv=f/K。表1是某一涡轮流量计出厂时的校验数据，其流量的计算表达式为：流量=频率÷平均仪表系数。虽然其精确度已经达到了1.5级，但在实验室条件和对精度要求比较高的场合中，1.5级并满足不了其精度要求。为了提高计算精度，现考虑采用多项式曲线拟合的方法，在其量程范围内用一个多项式近似代替比较复杂的解析表达式。根据傅立叶定律，在提高多项式次数的情况下即可得到更高的计算精度。

    结合表1的数据和式（6），对表1的数据分别进行了不同次数的多项式拟合。多项式拟合方法有许多，例如在MTALB中、Excell中均可实现数据的拟合。笔者为了计算方便及多方面的要求，使用VB语言编写了一个多项式拟合程序，拟合方法参考于文献[4]中曲线拟合部分。结果见表2。

    表2 不同仪表系数计算方法的比较

    通过表2的比较可以发现在使用一次多项式拟合的情况下，流量误差比原来平均减小了一半，在使用三次多项式拟合的情况下，流量误差则减小了一个数量级。精度有显著提高。